Фирма производит два популярных безалкогольных напитка лимонад и тоник

Задача 1. Решить графическим методом типовую задачу оптимизации

Фирма производит два широко популярных безалкогольных напитка - "Лимонад" и "Тоник". Фирма может продать всю продукцию, которая будет произведена. Однако объем производства ограничен количеством основного ингредиента и производственной мощностью имеющегося оборудования. Для производства 1 л "Лимонада" требуется 0,02 час работы оборудования, а для производства 1 л "Тоника" - 0,04 ч. Расход специального ингредиента составляет 0,01 кг и 0,04 кг на 1 л "Лимонада" и "Тоника" соответственно. Ежедневно в распоряжении Фирмы имеется 24 ч времени работы оборудования и 16 кг специального ингредиента. Прибыль фирмы составляет 0,1 ден. ед. за 1 л "Лимонада" и 0,3 ден. ед. за 1 л "Тоника". Сколько продукции каждого вида следует производит ежедневно, если цель фирмы состоит в максимизации ежедневной работы?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум и почему?

Составим ЭММ задачи:

В рамках заданных ограничений фирма должна принять решение о том, какое количество каждого вида напитков следует выпускать. Пусть x1 - число литров Лимонада, производимое за день. Пусть x2 - число литров Тоника, производимое за день.

Определение цели и ограничений. Цель состоит в максимизации ежедневного дохода. Пусть F(x) = 0,1x1 + 0,3x2 (max) - ежедневный доход, ден. ед. Он максимизируется в рамках ограничений на количество часов работы оборудования и наличие специального ингредиента. Это целевая функция задачи - количественное соотношение, которое подлежит оптимизации.

Существуют следующие ограничения на производственный процесс:

Время работы оборудования. Для производства х1 литров Лимонада и х2 литров Тоника требуется: (0,02 х1 + 0,04 х2) часов работы оборудования ежедневно. Максимальное время работы оборудования в день составляет 24 ч, следовательно, объем производства должен быть таким, чтобы число затраченных часов работы оборудования было меньше либо равно 24 ч ежедневно. Таким образом,

,02 х1 + 0,04 х2£ 24 ч/день.

Специальный ингредиент. Производство х1 литров Лимонада и х2 литров Тоника требует (0,01 х1 + 0,04 х2) кг ингредиента ежедневно. Максимальный расход ингредиента составляет 16 кг в день, следовательно, объем производства должен быть таким, чтобы требуемое количество специального ингредиента составляло не более 16 кг в день. Таким образом,

,01 х1 + 0,04 х2 £ 16 кг/день.

Окончательная формулировка задачи линейного программирования имеет следующий вид:

(x) = 0,1x1 + 0,3x2 (max)

,02 х1 + 0,04 х2 ≤ 24

,01 х1 + 0,04 х2 ≤ 16

Ограничения задачи можно изобразить графически.

Время работы оборудования:

,02 х1 + 0,04 х2 ≤ 24 ч/день.

,02 х1 + 0,04 х2 = 24

Простейшим способом нанесения прямой на график является нахождение точек пересечения данной прямой с осями координат х1 и х2. Подставив х1 = 0 в уравнение и рассчитав значение х1, получим, что при х1 = 0, х2 = 600. Подставив х2= 0 в уравнение и рассчитав значение х1, получим, что при х2 = 0 х1 = 1200. Нанесем эти две точки на график и соединим их прямой. Для определения области, которую следует заштриховать, подставим х1= 0 и х2 = 0 в неравенство: 0,02 х1 + 0,04 х2 ≤ 24

Специальный ингредиент: 0,01 х1 + 0,04 х2 ≤ 16

Проведем прямую: 0,01 х1 + 0,04 х2 = 16

Таким же образом, подставив х1 = 0 в уравнение и рассчитав значение х1, получим, что при х1 = 0, х2 = 400. Подставив х2= 0 в уравнение и рассчитав значение х1, получим, что при х2 = 0 х1 = 1600. Нанесем эти две точки на график и соединим их прямой. Для определения области, которую следует заштриховать, подставим х1= 0 и х2 = 0 в неравенство: 0,01 х1 + 0,04 х2 ≤ 16

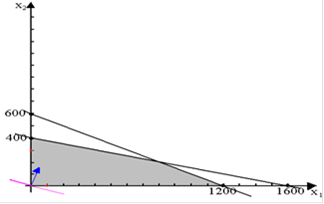
Область, отмеченная серым цветом - это допустимое множество,

которое содержит все возможные сочетания объемов производства, удовлетворяющие данным ограничениям. Координаты любой точки, принадлежащей допустимому множеству, являются возможным сочетанием объемов производства двух видов напитков, выпускаемых фирмой.

Важно! При покупке готовой работы
сообщайте Администратору код работы:

Соглашение

* Готовая работа (дипломная, контрольная, курсовая, реферат, отчет по практике) – это выполненная ранее на заказ для другого студента и успешно защищенная работа. Как правило, в нее внесены все необходимые коррективы.
* В разделе "Готовые Работы" размещены только работы, сделанные нашими Авторами.
* Всем нашим Клиентам работы выдаются в электронном варианте.
* Работы, купленные в этом разделе, не дорабатываются и деньги за них не возвращаются.
* Работа продается целиком; отдельные задачи или главы из работы не вычленяются.

С условиями соглашения согласен (согласна)

Цена: 1000 р. Купить эту работу

Содержание

ЗАДАЧА 1.

Решить графическим методом типовую задачу оптимизации.

ЗАДАЧА 2.

Предложить оптимальное управленческое решение в следующих типовых хозяйственных ситуациях.

2.10. Менеджер по ценным бумагам намерен разместить 100000 ф ст. капитала такимобразом, чтобы получать максимальные годовые проценты с дохода. Его выбор ограничен четырьмя возможными объектами инвестиций А, В, С и О. Объект А позволяет получать 6% годовых, объект В – 8% годовых, объект С – 10%, а объект О – 9% годовых. Для всех четырех объектов степень риска и условия размещения капитала различны. Чтобы не подвергать риску имеющийся капитал, менеджер принял решение, что не менее половины инвестиций необходимо вложить в объекты А и В. Чтобы обеспечить ликвидность, не менее 25% общей суммы капитала нужно поместить в объект О. Учитывая возможные изменения в политике правительства, предусматривается, что в объект С следует вкладывать не более 20% инвестиций, тогда как особенности налоговой политики требуют, чтобы в объект А было вложено не менее 30% капитала.

Как распорядиться свободными денежными средствами?

ЗАДАЧА 3.

Провести моделирование и решить специальную задачу линейного программирования.

Время выполнения,

Оценки даны бригадирами и опыт работы их в фирме дает основания руководству доверять им.

Распределить объекты работ между бригадами, чтобы общее количество человеко-дней, затраченное на выполнение работ на всех пяти объектах, было минимальным.

ЗАДАЧА 4.

Рассчитайте характеристики системы массового обслуживания. Во всех задачах предполагается, что поток требований является простейшим (пуассоновским), а продолжительность обслуживания распределена по экспоненциальному закону.

4.10. Оптовый склад обслуживает 30 предприятий-потребителей материалов. Каждое из предприятий направляет на склад автомашину в среднем один раз в смену (смена - 8 ч). Средняя продолжительность погрузки одной автомашины составила 48 мин, т.е. 0,1 смены. Погрузка осуществляется кранами. Потери склада, связанные с простоем крана (включая крановщика и стропальщиков) из-за отсутствия автомашин, равны 5 у.е./ч.

Прибывшая на склад автомашина становится в очередь, если все краны заняты погрузкой других автомашин. При этом склад оплачивает предприятиям расходы, связанные с простоем на складе их автомашин и шоферов в очереди под погрузку, из расчета 2,6 у.е. за час простоя автомашины и шофера. Определите:

1) оптимальное количество необходимых складу кранов, при котором суммарные ожидаемые потери склада, связанные с простоем кранов (из-за отсутствия автомашин) и простоем автомашин в очереди, были бы минимальными;

2) коэффициент простоя крана;

3) среднее число автомашин, находящихся в очереди (длину очереди);

4) коэффициент и среднее время простоя автомашины в очереди.

Указание: для определения оптимального количества кранов необходимо рассчитать при разном их количестве коэффициенты простоя кранов и коэффициенты простоя автомашин в очереди. Например, при четырех кранах коэффициент простоя автомашин будет равен 0,0172, а коэффициент простоя кранов - 0,3299. Тогда потери от простоев кранов и автомашин (если потери от простоя одного крана равны 5 у.е./ч, а одной автомашины - 2,6 у.е./ч) при четырех кранах составят 2,6×30×0,0172 + 5×4×0,3299 = 7,94 у.е. Оптимальное количество кранов будет соответствовать минимальной сумме потерь.

ЗАДАЧА 5.

Задачи управления проектами

5.10. Какое количество товара заказывать и по какой цене, каковы затраты при оптимальной организации управления затратами? Известно, что интенсивность потребления товара 240 штук/день; затраты на оформление заказа K =30 руб.; затраты на хранение запаса s = 3 руб. /шт.*дн.; исходная цена C = 6 руб./шт.; цена с первой скидкой 5 руб./шт.; цена со второй скидкой 3 руб./шт.; точки разрыва цен ; шт.

Цена: 1000 р. Купить эту работу

ЭММ.doc

Министерство образования и науки РФ

Федеральное агентство по образованию ГОУ ВПО

Всероссийский заочный финансово- экономический институт

Специальность: Финансы и Кредит

Группа: 3 курс (2 поток)

Краснодар 2009 г.

Задача 1.

Решить графическим методом типовую задачу оптимизации.

Решение.

Экономико-математическая модель задачи:

Х₁	Х₂	ИТОГО
Время работы оборудования	0,02	0,04	24
Расход ингредиента	0,01	0,04	16
Прибыль фирмы	0,1	0,3

Введем целевую функцию: F(X) = 0,1 x₁+0,3 x₂ max

Первое ограничение (по времени работы оборудования) имеет вид: 0,02х₁ + 0,04 х₂ 24. Находим пересечение с осями координат. Прямая 0,02х₁ + 0,04 х₂ = 24 проходит через точки (1200;0) и (0;600). Второе ограничение (по расходу ингредиента) имеет вид 0,01х₁ + 0,04 х₂ 16. Найдем пересечение с осями координат. Прямая 0,01х₁ + 0,04 х₂ = 16 проходит через точки (1600;0) и (0;400). Решением этих неравенств системы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. В результате пересечения построенных полуплоскостей получаем многоугольник, который и является областью допустимых значений данной задачи. (рис. 1.)

Рис. 1. Область допустимых значений.

Построим вектор-градиент. Начало вектора совпадает с началом координат. Построим линию уравнения, перпендикулярную вектору – градиента: 0,1x₁+0,3x₂ = 0. При максимизации функции движемся в направлении вектора-градиента.

Реши систему уравнений:

Получаем: x₁ = 800; x₂ = 200. При этих значениях f_max = f (800;200) = 0,1*800 +0,3*200=140.

Ответ.

Задача 2.

Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования.

Для изготовления трех видов продукции используют четыре вида ресурсов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Вид ресурсов	Нормы расхода ресурсов на ед. продукции			Запасы ресурсов
Вид ресурсов	I вид	II вид	III вид	Запасы ресурсов
Труд	3	6	4	2000
Сырье 1	20	15	20	15000
Сырье 2	10	15	20	7400
Оборудование	0	3	5	1500
Цена изделия	6	10	9

Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
Пояснить нулевые значения переменных в оптимальном плане.
На основе свойств двойственных оценок и теорем двойственности:

Проанализировать использование ресурсов в оптимальном плане исходной задачи;

Определить, как изменится выручка и план выпуска продукции при увеличении запаса ресурса первого вида на 24 единицы;
Оценить целесообразность включения в план изделия четвертого вида ценой 11 единиц, если нормы затрат ресурсов 8, 4, 20 и 6 единиц.

Решение.

Введем переменные: Х₁ – норма расхода ресурсов на ед.продукции I вида; Х₂ – норма расхода на ед.продукции II вида; Х₃ – норма расхода на ед.продукции III вида.

Введем целевую функцию: F(X) = 6 x₁+10 x₂ + 9 х₃ max

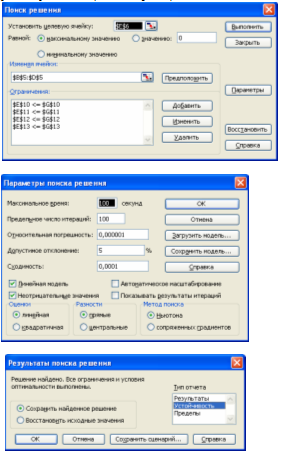
Для решения задачи воспользуемся программой Excel. Сначала необходимо ввести исходные данные, далее устанавливаем зависимость для целевой функции. После этого вводим зависимости для ограничений и запускаем команду поиск решений (рис. 2.)

Рис. 2. Поиск решения.

В результате данного решения было выявлено, что для получения максимальной прибыли в размере 4110 ден.ед. фирма должна производить 520 единиц продукции I вида и 110 единиц продукции II вида. Также было выявлено, что сырья 1 понадобиться лишь 12 600, вместо 15 000, а оборудования задействовано лишь 550, вместо 1500. Трудовые ресурсы и сырье 2 будет использовано полностью (рис. 3).

Рис. 3. Результаты поиска решения.

В отчете по результатам (рис. 4.) содержатся оптимальные значения переменных х₁, х₂, х₃, которые равны 520;0;110 соответственно; значение целевой функции (4110 ед.), а также левые части ограничений.

Рис. 4. Отчет по результатам решения.

Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.

Вводим переменные: исходная задача содержит 4 ограничения: по труду, по сырью 1, по сырью 2, по оборудованию. Следовательно, в двойственной задачи – 4 переменные.

Целевая функция двойственной задачи формулируется на минимум. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи:

Вводим ограничения. В исходной задаче 3 переменные, следовательно, в двойственной задачи 3 ограничения. В правых частях ограничений двойственной задачи стоят коэффициенты при неизвестных в целевой функции исходной задачи. Левая часть ограничений определяет стоимость ресурсов, затраченных на производство единицы продукции. Каждое ограничение соответствует определенной норме использования ресурса на единицу продукции:

Определим оптимальный план двойственной задачи, используя теоремы двойственности.

Воспользуемся первым соотношением второй теоремы двойственности

Подставим оптимальные значения вектора * = (520;0;110) в полученные выражения:

y₁(3* 520+ 6*0+ 4*110 – 2000) = 0;

y₂(20*520 + 15*0 + 20*110 – 15000) = 0;

y₃(10*520 + 15*0 + 20 *110 – 7400) = 0;

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Всероссийский заочный финансово-экономический институт

Список использованной литературы…………………………………..30

Решить графическим методом типовую задачу оптимизации.

max f ( ) = 0,10x 1 + 0,30x 2

при условии выполнения ограничений:

Решаем задачу графическим методом:

Областью допустимых решений системы является многоугольник ОАВС.

Построим линию уровня 0,10 x 1 + 0,30 x 2 и вектор .

При перемещении линии уровня в направлении вектора значении функции возрастает. Наибольшее значение достигается в точке B.

x 1 + 4·200 = 1600

Проверим правильность расчетов с помощью средств MS Excel:

1. Ввели зависимость для целевой функции и ограничений:

3. Из меню Сервис выберали Поиск решения.

Назначили целевую функцию, ввели ограничения и на вкладке Параметры установили Линейная модель и Неотрицательные значения.

4. Щелкнули Выполнить.

При решении задачи на min линию уровня следует сдвигать в противоположную сторону от вектора . Наименьшее значение будет достигнуто в точке О (0;0). Значит x 1 = 0, x 2 = 0, . Это значит, что не надо ничего выпускать и прибыль будет равна 0.

Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования.

Нормы расхода ресурсов на единицу продукции

Пример решения типовой задачи оптимизации графическим методом. Получение оптимального плана выпуска продукции при помощи теории двойственности. Применение метода Леонтьева для построения баланса производства и распределения продукции предприятий.

Рубрика	Экономико-математическое моделирование
Вид	контрольная работа
Язык	русский
Дата добавления	23.04.2013

Министерство образования и науки РФ

Федеральное агентство по образованию ГОУ ВПО

Всероссийский заочный финансово-экономический институт

кафедра экономико-математических методов и моделей

по дисциплине: Экономико-математические методы и прикладные модели

факультет менеджмент и маркетинг

специальность менеджмент организации

студентки 3-го курса группы

Гармаш Александр Николаевич

Задача 1. Решить графическим методом типовую задачу оптимизации

Составим ЭММ задачи:

В рамках заданных ограничений фирма должна принять решение о том, какое количество каждого вида напитков следует выпускать. Пусть x1 -- число литров Лимонада, производимое за день. Пусть x2 -- число литров Тоника, производимое за день.

Определение цели и ограничений. Цель состоит в максимизации ежедневного дохода. Пусть F(x) = 0,1x1 + 0,3x2 (max) -- ежедневный доход, ден. ед. Он максимизируется в рамках ограничений на количество часов работы оборудования и наличие специального ингредиента. Это целевая функция задачи -- количественное соотношение, которое подлежит оптимизации.

Существуют следующие ограничения на производственный процесс:

Время работы оборудования. Для производства х 1 литров Лимонада и х 2 литров Тоника требуется: (0,02 х 1 + 0,04 х 2 ) часов работы оборудования ежедневно. Максимальное время работы оборудования в день составляет 24 ч, следовательно, объем производства должен быть таким, чтобы число затраченных часов работы оборудования было меньше либо равно 24 ч ежедневно. Таким образом,

0,02 х1 + 0,04 х2Ј 24 ч/день.

Специальный ингредиент. Производство х 1 литров Лимонада и х2 литров Тоника требует (0,01 х 1 + 0,04 х2) кг ингредиента ежедневно. Максимальный расход ингредиента составляет 16 кг в день, следовательно, объем производства должен быть таким, чтобы требуемое количество специального ингредиента составляло не более 16 кг в день. Таким образом,

0,01 х1 + 0,04 х2 Ј 16 кг/день.

Окончательная формулировка задачи линейного программирования имеет следующий вид:

F(x) = 0,1x1 + 0,3x 2 (max)

0,02 х1 + 0,04 х 2 ? 24

0,01 х 1 + 0,04 х 2 ? 16

Ограничения задачи можно изобразить графически.

Время работы оборудования:

0,02 х1 + 0,04 х 2 ? 24 ч/день.

0,02 х1 + 0,04 х 2 = 24

Простейшим способом нанесения прямой на график является нахождение точек пересечения данной прямой с осями координат х 1 и х 2 . Подставив х 1 = 0 в уравнение и рассчитав значение х 1 , получим, что при х 1 = 0 , х 2 = 600. Подставив х 2 = 0 в уравнение и рассчитав значение х 1 , получим, что при х 2 = 0 х 1 = 1200. Нанесем эти две точки на график и соединим их прямой. Для определения области, которую следует заштриховать, подставим х 1 = 0 и х 2 = 0 в неравенство: 0,02 х 1 + 0,04 х 2 ? 24

Специальный ингредиент: 0,01 х 1 + 0,04 х 2 ? 16

Проведем прямую: 0,01 х 1 + 0,04 х 2 = 16

Таким же образом, подставив х 1 = 0 в уравнение и рассчитав значение х 1 , получим, что при х 1 = 0, х 2 = 400. Подставив х 2 = 0 в уравнение и рассчитав значение х 1 , получим, что при х 2 = 0 х 1 = 1600. Нанесем эти две точки на график и соединим их прямой. Для определения области, которую следует заштриховать, подставим х 1 = 0 и х 2 = 0 в неравенство: 0,01 х 1 + 0,04 х 2 ? 16

Область, отмеченная серым цветом -- это допустимое множество , которое содержит все возможные сочетания объемов производства, удовлетворяющие данным ограничениям. Координаты любой точки, принадлежащей допустимому множеству, являются возможным сочетанием объемов производства двух видов напитков, выпускаемых фирмой.

Решим систему уравнений

Вычтем уравнение (2) из уравнения (1): 0,01 х 1 = 8.

Тогда х 1 = 800 л в день. Подставив найденное значение х 1 в уравнение (2), найдем х 2 :

0,01 * 800 + 0,04 х 2 = 16.

х 2 = 200 л в день.

max F(х_1,х₂) = 0,1* 800 + 0,3 * 200 = 140 (ден. ед.)

Ответ: Максимальная ежедневная прибыль от реализации продукции составит 140 ден.ед. при производстве 800 л "Лимонада" и 200 л "Тоника". Если решать задачу на минимум, то компания прибыли не получит и при производстве продукции понесет убытки.

Задача 2. Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования

Для изготовления трех видов продукции используют четыре вида ресу р сов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого в и да продукции приведены в таблице.

Тема: Контрольная по Методам оптимальных решений Вариант 10

Тип: Контрольная работа | Размер: 86.30K | Скачано: 162 | Добавлен 09.06.13 в 21:10 | Рейтинг: +3 | Еще Контрольные работы

Вуз: Финансовый университет

Год и город: Москва 2013

ЗАДАЧА 1

Решить графическим методом типовую задачу оптимизации.

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум и почему?

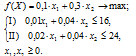
Задачу решаем графическим методом.

Строим область допустимых решений задачи (см. рисунок). Данные для ее построения приведены в таблице:

Точки для построения граничной прямой

Выполнение неравенства в контрольной точке (0; 0)

Стоим вектор-градиент целевой функции задачи. За его начало принимаем точку (0; 0), тогда концом вектора-градиента будет являться точка с координатами, равными коэффициентам целевой функции по соответствующим координатным осям — (0,1; 0,3). Перпендикулярно вектору-градиенту через точку его начала строится линия нулевого уровня целевой функции — прямая, в каждой точке которой целевая функция принимает нулевое значение: f(X)=0.

Для определения положения точки максимума целевой функции линия, параллельная линии нулевого уровня, смещается в направлении вектора-градиента, до тех пор, пока она не покинет область допустимых решений. Предельная точка области допустимых решений при этом движении и является точкой максимума.

В нашей задаче — это точка B, образованная пересечением граничных прямых ограничений I и II. Ее координаты определяются решением системы уравнений этих прямых:

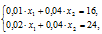
Таким образом, для получения максимально возможной в данных условиях выручки 140 руб. следует производить 800 л напитка “Лимонад” X₁ и 200 л напитка “Тоник” X₂.

Решение данной задачи линейного программирования на минимум лишено экономического смысла, так как выручку от реализации продукции стремятся получить наибольшей, а не наименьшей. Однако математически эта задача имеет решение и на минимум: наименьшее значение в области допустимых решений целевая функция принимает в точке (0; 0), и это значение равно

ЗАДАЧА 2

Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования

Для изготовления трех видов продукции используют четыре вида ресурсов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Нормы расхода ресурсов на ед. продукции

Требуется:

Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.

Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.

Пояснить нулевые значения переменных в оптимальном плане.

На основе свойств двойственных оценок и теорем двойственности:

проанализировать использование ресурсов в оптимальном плане исходной задачи;

определить, как изменятся выручка и план выпуска продукции при увеличении запаса ресурса первого вида на 24 единицы;

оценить целесообразность включения в план изделия четвертого вида ценой 11 денежных единиц, если нормы затрат ресурсов 8, 4, 20 и 6 единиц.

Решение. 1. Данная задача оптимизации является задачей линейного программирования. Обозначим количество выпускаемых единиц продукции I, II, III соответственно как х₁, х₂, х₃. Целевой функцией задачи является общая стоимость выпускаемой продукции, которая должна быть наибольшей. Число ограничений задачи равно числу ресурсов, используемых для изготовления изделий — 4. Дополнительно вводится условие неотрицательности переменных. Зная цены изделий, нормы их расхода и запасы ресурсов, формулируем математическую модель исходной задачи линейного программирования:

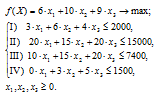
(для копирования снимка окна в буфер обмена данных используется комбинация клавиш Alt + Print Screen).

Использование надстройки позволило получить значения переменных оптимального плана выпуска изделий: Х*=(520; 0; 110). Целевая функция имеет наибольшее для данных условий задачи значение f(X*)=4110 (прил. 1).

Таким образом, для получения наибольшей выручки от реализации продукции следует производить x₁*=520 изделий I, x₃*=110 изделий III и не производить изделия II (x₂*=0).

2. Обозначим двойственные оценки ресурсов I, II, III, IV как y₁, y₂, y₃, y₄ соответственно. Целевой функцией двойственной задачи является общая стоимость запасов ресурсов в двойственных оценках, которая должна быть наименьшей. Число ограничений двойственной задачи равно числу переменных исходной задачи — 3. Математическая модель двойственной задачи имеет вид:

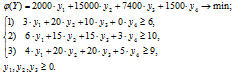
Наименьшее значение целевой функции двойственной задачи

совпадает (в пределах погрешности округления) с наибольшим значением целевой функции исходной задачи f(X*).

3. Выпуск изделий II невыгоден для данных условий задачи. Это объясняется тем, что стоимость ресурсов на изготовление единицы этой продукции в теневых ценах превышает цену реализации:

4. Проанализируем использование ресурсов в оптимальном плане. Для этого подставим в ограничения исходной задачи значения переменных оптимального плана Х*=(520; 0; 110) и проверим выполнение неравенств:

Видно, что ресурсы I и III используются в оптимальном плане полностью, т. е. являются дефицитными. На это обстоятельство указывает и то, что теневые цены этих ресурсов больше нуля (y₁*>0; y₃*>0). Самым дефицитным является ресурс I, так как он имеет наибольшую теневую цену (y₁*=1,5); наименее дефицитен ресурс III (y₃*=0,15).

Ограниченные запасы дефицитных ресурсов I и III сдерживают рост объемов выпускаемой продукции и наибольшей выручки от ее реализации. Увеличение объема ресурса I на одну единицу при неизменных объемах других ресурсов ведет к росту наибольшей выручки на 1,5 руб., увеличение объема ресурса III на единицу — на 0,15 руб.

Ресурсы II и IV являются недефицитными (y₂*=0; y₄*=0), т. е. избыточными в оптимальном плане. Увеличение объемов этих ресурсов не повлияет на оптимальный план выпуска продукции и не увеличит ее общую стоимость.

Для определения целесообразности включения в план выпуска еще и изделия IV с заданными характеристиками рассчитаем стоимость ресурсов на изготовление единицы этого изделия в теневых ценах и сравним это значение с ценой реализации:

Следовательно, продукцию IV выпускать невыгодно, так как она поглощает часть дефицитных ресурсов и тем самым сдерживает рост выпуска выгодной продукции. Это, в свою очередь, препятствует увеличению общей стоимости выпускаемых изделий. Если бы изделие IV реализовывалось по цене равной или большей 15 руб., то его производство было бы выгодным.

1) рабочий лист EXCEL;

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы

Читайте также:

Аренда холодильников для напитков бесплатно при покупке напитков
Бойлеры для приготовления горячих напитков
Ложка для приготовления смешанных напитков
Кружки для горячих напитков с собой
Как приготовить кофе с корицей для похудения в домашних условиях