Как решить задачу каши

Решение: Данное уравнение является линейным дифференциальным уравнением первого порядка следующего вида:

Решим уравнение методом Лагранжа. Сначала найдём общее решение соответствующего однородного уравнения

Решение неоднородного уравнения ищем в виде

Таким образом, получим общее решение неоднородного уравнения:

Используя начальное условие, определим значение произвольной постоянной

Следовательно частное решение исходного уравнения имеет вид

Задача, в которой требуется найти частное решение уравнения y' = f(х, у) удовлетворяющее начальному условию у(х0) = y0, называется задачей Коши.

Построенный на плоскости хОу график всякого решения у = φ(х) дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению у = φ(х, С) на плоскости хОу соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной С, а частному решению, удовлетворяющему начальному условию y(x0) = y0, – кривая этого семейства, проходящая через заданную точку М0(x0; у0).

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах… Ч. II.

Онлайн калькулятор для решения задачи Коши. Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Для того чтобы решить задачу Коши необходимо найти общее решение дифференциального уравнения, а потом подставить начальные условия и найти неизвестные коэффициенты С1 и С2.
Данный калькулятор решает задачу Коши для дифференциального уравнения второго порядка.
В калькулятор вводим дифференциальное уравнение и начальные условия, как указано в примере, нажимаем кнопку "Вычислить", получаем ответ.

Рассмотрим пример решения задачи Коши с помощью онлайн калькулятора "Контрольная-работа.Ру".

Внимание! Следуя этому примеру и подробно и внимательно читая вы сможете решить и свою задачу, просто следуя тем же шагам!

Возьмём задачу из контрольной "Решить задачу Коши для дифференциального уравнения второго порядка":

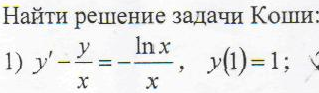
Для того, чтобы решить данную задачу откройте сервис решения дифференциальных уравнений онлайн

и введите в форму левую часть уравнения y' - y/x

а в правую часть уравнения: -lnx/x

как на картинке:

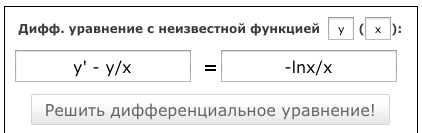
Нажимаем кнопку "Решить дифференциальное уравнение!"

Видим ответ для этого дифф. ур-ния:

Но как вы знаете, это ещё не решение задачи Коши, это всего лишь решение дифференциального уравнения.

Теперь по начальным условиям y(1) = 1 надо найти C1.

Для этого воспользуемся сервисом по решению обычных уравнений онлайн

Вобъём в форму обычных уравнений в правую часть уравнения c*x + log(x) + 1, а в левую y

А также укажем, что уравнение с неизвестной c=C1

На рис. всё это видно:

Нажимаем кнопку "Решить уравнение!"

Получаем ответ для C1

Но и это ещё не всё.

Надо указать, что y = 1 и x = 1 (т.к. y(1)=1). Подставляем по той же ссылке как на рис. ниже:

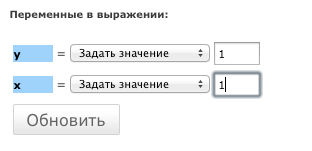
Нажимаем кнопку "Обновить"

И получаем окончательный ответ для C1:

Подставляем это C1 в решение дифф. уравнения и мы получим решение нашей задачи Коши:

Тэги: уравнение

Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию этой переменной и её производные (или дифференциалы) различных порядков.

Порядком дифференциального уравнения называется порядок старшей производной, содержащейся в нём.

Примеры дифференциальных уравнений:

Уравнение (1) - четвёртого порядка, уравнение (2) - третьего порядка, уравнения (3) и (4) - второго порядка, уравнение (5) - первого порядка.

Дифференциальное уравнение n-го порядка не обязательно должно содержать явно функцию, все её производные от первого до n-го порядка и независимую переменную. В нём могут не содержаться явно производные некоторых порядков, функция, независимая переменная.

Например, в уравнении (1) явно нет производных третьего и второго порядков, а также функции; в уравнении (2) - производной второго порядка и функции; в уравнении (4) - независимой переменной; в уравнении (5) - функции. Только в уравнении (3) содержатся явно все производные, функция и независимая переменная.

Решением дифференциального уравнения называется всякая функция y = f(x), при подстановке которой в уравнение оно обращается в тождество.

Процесс нахождения решения дифференциального уравнения называется его интегрированием.

Это и есть решение данного дифференциального уравнения. Меняя в нём C, будем получать различные решения. Мы выяснили, что существует бесконечное множество решений дифференциального уравнения первого порядка.

Общим решением дифференциального уравнения n-го порядка называется его решение, выраженное явно относительно неизвестной функции и содержащее n независимых произвольных постоянных, т. е.

Решение дифференциального уравнения в примере 1 является общим.

Частным решением дифференциального уравнения называется такое его решение, в котором произвольным постоянным придаются конкретные числовые значения.

Решение. Проинтегрируем обе части уравнения такое число раз, которому равен порядок дифференциального уравнения.

В результате мы получили общее решение -

данного дифференциального уравнения третьего порядка.

Теперь найдём частное решение при указанных условиях. Для этого подставим вместо произвольных коэффициентов их значения и получим

Записываем решение задачи Коши для данного дифференциального уравнения первого порядка:

При решении дифференциальных уравнений, даже самых простых, требуются хорошие навыки интегрирования и взятия производных, в том числе сложных функций. Это видно на следующем примере.

Решение. Уравнение записано в такой форме, что можно сразу же интегрировать обе его части.

Требуется взять dx и теперь - внимание - делаем это по правилам дифференцирования сложной функции, так как x и есть сложная функция ("яблоко" - извлечение квадратного корня или, что то же самое - возведение в степень "одна вторая", а "фарш" - самое выражение под корнем):

Возвращаясь к переменной x, получаем:

Это и есть общее решение данного дифференциального уравнения первой степени.

Не только навыки из предыдущих разделов высшей математики потребуются в решении дифференциальных уравнений, но и навыки из элементарной, то есть школьной математики. Как уже говорилось, в дифференциальном уравнении любого порядка может и не быть независимой переменной, то есть, переменной x. Помогут решить эту проблему не забытые (впрочем, у кого как) со школьной скамьи знания о пропорции. Таков следующий пример.

то есть, в нём в некотором виде появился x.

то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.

Применяя это свойство, преобразуем уравнение к виду

после чего интегрируем обе части уравнения:

Оба интеграла - табличные, находим их:

и получаем решение данного дифференциалного уравнения первого порядка:

Эта статья представила необходимый минимум сведений о дифференциальных уравнениях и их решениях и должна помочь вам уверенно и увлечённо перейти к изучению различных видов дифференциальных уравнений.

Принцип и понятие

Под задачей Коши для дифференциального уравнения понимают выражение вида: y' = f (x, y) с начальным условием, соответствующим равенству: y (x0) = y0. По сути, это обозначает, что необходимо найти такое решение уравнения, которое проходит через заданную точку игрек и икс нулевое. Решением задачи называется функция, заданная на указанном интервале в окрестности точки икс нулевое, то есть: x Є (x0 — q, x0 + q).

Для проведения анализа функции должны выполняться следующие критерии:

• y (x0) = y0;
• y' = f (x, y (x));
• V x Є (x0 — q, x0 + q).

Следует отметить, что решение Коши включает в себя и сам интервал икс нулевое плюс минус кью, фактически q-окрестность. Это обозначает, что одна и та же функция, задаваемая одной формулой, но рассматриваемая на разных интервалах, представляет два разных нахождения задачи Коши. Отсюда возникает вопрос, при каких же ответах существует решение Коши, а также когда оно будет единственным.

Существует теорема, гарантирующая единственность какого-то решения задачи. На самом деле возможность аналитического подхода Коши требует лишь главного условия, при котором функция f будет непрерывной в какой-то окрестности точки x0, y0. Но для доказательства единственности этого недостаточно. Для нормального случая необходимо следующее:

1. Функция f (x, y) непрерывна в некоторой окрестности точки (x0, y0).
2. Существует такая константа C, что для любых точек икс и игрек выполняется неравенство: |f (x, y) — f (x2, y2)| ⩽ C |y1 — y2|.

По игреку функция должна иметь обыкновенный рост, то есть не убыстряющийся (локальный подъём не превышать линейный). Если эти два условия выполняются, то решение Коши существует и оно будет единственным. Это значит, что тогда у точки икс нулевое найдётся такая окрестность, в которой существует решение и к тому же оно будет единственным.

А это обозначает, что любая другая функция в этой окрестности, удовлетворяющая уравнениям начальных условий, совпадает с той, существование которой утверждается. При этом на практике проверка условия на самом деле вещь не очень сложная, особенно если функция f (y) имеет в окрестности ограниченную производную.

Алгоритм нахождения

Пусть имеется функция у' = 2 * √ |y| и условие что y (0) = 0. Необходимо её исследовать. Тут можно заметить, что в этом случае функция зависит только от игрека и условию не удовлетворяет. В окрестностях точки с координатами (0, 0) она не удовлетворяет условию, так как любая окрестность захватывает ноль, а у корня квадратного по игреку будет бесконечная производная.

Это приводит не к единственности получения результатов. Так, у уравнения есть два решения: y1 тождественный нулю; y2 равняется x2. Согласно условию, игрек стоит по модулю, точнее, можно сказать, что для отрицательных значений икс будет меньше ноля, а положительных — больше.

Главный же вопрос заключается в продолжаемости анализа. Доказывается возможность простым построением решения с использованием специальных условий. В итоге должна быть найдена окрестность в точке x0. То есть берётся уравнение и точка с начальными координатами, затем выясняется, что в окрестности выполнены условия теоремы и строится решение.

Затем исследуется другая точка и изучается структура её окрестности. Например, обнаруживается, что условия существования единственности выполняются. Согласно теореме, тогда можно будет строить решение, где в качестве начальной точки будет взята любая координата. Другими словами, получается более широкое решение. Поэтому возникает вопрос, насколько можно приблизить точность ответа. Практические примеры показывают, что иногда можно двигаться до бесконечности, а в некоторых случаях сделать не более трёх шагов.

Если есть два уравнения y' = f (x, y); y (x0) = y0 имеющие два решения: y1 (x), x Є I1 (эX), y2 (x), x єI2 (єX0). Тогда можно утверждать, что игрек два будет продолжением решения y1 (x) если в I2 входит I1, а y2 (x) равняется y1 (x) для любого икс из интервала I1. Следует учесть, что в этом определении в качестве областей функции всегда рассматривается интервал.

В изучении исследуются и матричные функциональные системы, состоящие из нескольких переменных A (z 1, z 2, …, zn). При этом z являются вещественными, а элементы матрицы могут быть как вещественными, так и комплексными. Исходя из этого даётся определение того, что функция, описываемая матрицей, непрерывна тогда, когда все элементы непрерывны в точке или на некотором множестве.

При определении используют численные и векторные функции от аргумента: y = (x), где y — это столбец от набора игреков, а икс со штрихом — от набора иксов. Таким образом, обобщённым решением будет такое действие, которое не будет иметь нетривиального продолжения, то есть вторые интервалы содержать первые.

Примеры задач

На практических занятиях по высшей математике студентам предлагается для понимания курса выполнить ряд практических заданий. Существует типовой набор задач, научившись решать которые учащийся досконально разберётся в теме. Вот некоторые из них.

Первый пример. Имеется уравнение y' = (2y / x lnx) + 1/x, для которого установлено начальное условие y (e) = 0. Необходимо найти решение, проходящее через точку e. Перед тем как приступить непосредственно к решению, необходимо отметить, что функция f (x, y) определённа всюду, за исключением прямых x = 0 и x = 1. Отсюда следует, что краевое решение не может быть вычислено на интервале от нуля до единицы.

В этом примере должен содержаться интервал, имеющий координату точки e по иксу. Он не может включать значения меньше единицы, так как необходимо, чтобы выполнялось заданное условием уравнение, которое в точке x = 1 теряет смысл, ведь в ней функция неопределённа. Установив это, можно переходить к анализу уравнения.

Заданное равенство является линейным — неоднородным уравнением первого порядка. Для решения нужно сначала рассмотреть левое соотношение: y' = 2y / x * lnx. Добавив константу, уравнение можно переписать как y = c * e. Теперь необходимо взять интеграл исходя из первообразной формулы: ∫ 2 dx / (x *lnx).

После того как будет найдена постоянная, через общий интегральный метод с учётом условия определения функции, уравнение в окрестности точки e будет иметь решение вида: y = ln2x — lnx. Из полученного выражения можно сделать вывод, что функция будет определена для всех положительных иксов, но рассматривать её необходимо от единицы до плюс бесконечности. Это и будет максимальное непродолжаемое решение задачи: xЄ (1, + ∞).

Второй пример. Пусть имеется функция y' = y / (1+x 2 ) с начальным условием: y = y (0). В задании нужно будет рассмотреть дифференциальную кривую уравнения, проходящего через точку y0. Нужно заметить, что функция f (x, y) в любой ограниченной области двумерной плоскости удовлетворяет условию регулярности для теоремы существования единственности. В задаче спрашивается, каким должен быть y0, если предел максимального решения при иксе, стремящемся к плюс бесконечности, равняется единице.

Учитывая, что в этой постановке заложено, чтобы решение было определённо до плюс бесконечности и то, что уравнение является однородно линейным, по общей формуле особое решение будет иметь вид: y = c * e arctgx . Игрек нулевое не может равняться нулю, ведь в ином случае решением уравнения будет тождественный ноль и заданное условие выполняться не будет. В итоге получится, что y = y0 * e arctgx . Это решение и является подходящей функцией для любого интервала.

Операционный метод

Решение задачи Коши (примеров) целесообразно выполнять экономичным методом интегрирования линейных выражений, содержащих постоянные коэффициенты. Суть способа сводится к решению алгебраических равенств или неравенств. Алгоритм исследования заключается в следующих действиях:

1. Функции Y (p) и F (p) обозначают как изображения для y (x) и f (x).
2. Используя главные преобразования Лапласа, обрабатывая изображения, получают (pn (Yp) — p n -1 y 0 — …- yn -1) + a 1 (p n -1 y (p) — p n -2 y 0 — … — yn -2) + … + anY (p) = F (p) или, A (p)Y (p)+B (p) = F (p), причём A (p) и B (p) являются многочленами.
3. Найденное решение y (p) = (F (p) — B (p)) / A (p) и будет искомым y (x) для искомого y (p).

Например, пусть необходимо решить уравнение вида: x'' + 4x = sin (2t), при x (0) = 1, x'(0) = -2. Классическим методом находить ответ довольно трудоёмко, поэтому имеет смысл для заданного уравнения использовать операционное исчисление. Для начала следует ввести замену Lx = x. Затем к обеим частям равенства применить преобразование Лапласа: Lx '' + L 4 x = L * sin (2 t). Отсюда: Lx = x, Lx '' = p 2 x — px (0) — x'(0). Функция Лапласа используется для преобразования вещественной переменной в выражение с комплексной переменной и наоборот. Это и позволяет использовать её при решениях дифференциальных уравнений и систем.

На следующем этапе нужно подставить исходные данные в равенство: Lx'' = p 2 x — p + 2. Далее, следует выполнить преобразование и выразить неизвестную функцию. В итоге должно получиться выражение: X = (p 3 — 2 p 2 — 4 p — 6) / (p 2 + 4) 2 . Теперь можно найти оригинал изображений: x = L-1 <(p3 — 2p2 + 4p — 6) / (p2+4)2)>= cos (2t) — sin (2t) + (sin (2t) — 2tcos (2t))/8.

Использование онлайн-калькулятора

Часто решение задач по рассматриваемой теме связано с большими трудозатратами. Это касается времени и повышенного внимания. На практике не всегда получается правильно применить алгоритм и избежать ошибок. Поэтому имеет смысл для сложных заданий использовать онлайн-калькулятор. Решения на задачу Коши с его помощью доступны любому заинтересованному, имеющему доступ к интернету и устройство, поддерживающее работу веб-обозревателя.

В интернете существует довольно большое количество различных математических онлайн-решителей. В своём большинстве они бесплатны и ориентированы на работу даже с людьми, совершенно не разбирающимися в тематике. Поэтому они привлекательны не только как инструмент, предоставляющий быстрый и правильный ответ на поставленную задачу, но и как обучающие программы.

Всё дело в том, что на страницах сервисов, предлагающих такого рода услуги, содержится вся необходимая теоретическая информация. Кроме этого, они предлагают к рассмотрению типовые примеры с подробным объяснением решения. Из онлайн-калькуляторов, предоставляющих бесплатный доступ к своим услугам в русском сегменте интернета, можно отметить следующие:

1. Math.semestr.
2. Allcalc.
3. Kontrolnaya-rabota.
4. Matematikam.
5. Primat.

Для правильной записи уравнения существуют подсказки, так что разобраться, как работает сайт, сможет пользователь даже со слабой компьютерной подготовкой. Кроме этого, некоторые сервисы предлагают не просто ответ, а и пошаговое решение, к которому даётся комментарий. Решив несколько заданий, учащийся сможет разобраться в алгоритме и вычислять уравнения уже самостоятельно.

Следует отметить, что предложенные сервисы могут находить ответ для любой сложности математической задачи, например, вычисляя устойчивость математических моделей. Они также востребованы в инженерии и научных исследованиях, связанных с анализом функций. Для таких расчётов важны точность и время, что вполне могут обеспечить математические онлайн-сервисы.

Найти решения дифференциального уравнения: y' = f(x,y) (1) ,
удовлетворяющие условиям
y(x₀) = y₀, (2)
Сформулированные условия называются условиями Коши, а задача о выделении решения, удовлетворяющего условиям Коши - задачей Коши.

Назначение сервиса . Онлайн калькулятор можно использовать для проверки решения задачи Коши вида y' = f(x,y) .

• Решение онлайн
• Видеоинструкция

Определение . Будем говорить, что функция f(x,y) удовлетворяет условию Липшица по y в области D, если для любых двух точек (x,y₁), (x,y₂) из этой области выполнено неравенство:
|f(x,y₁) - f(x,y₂)| ≤ L|y_{1 -} y₂|, (3)
где L- некоторая константа, не зависящая от x.

Теорема . (существования и единственности). Пусть в уравнении (1) y' = f(x,y) функция f(x,y), заданная в области D на плоскости, непрерывна по x и удовлетворяет условию Липшица (3) по y. Тогда для любой точки (x₀, y₀)∈D существуют интервал (x₀ - λ, x₀ + λ) и функция y = φ(x) заданная на этом интервале так, что y = φ(x) есть решение уравнения, удовлетворяющее условию (2). Это решение единственно в том смысле, что если y = φ(x) есть решение уравнения (1) определенное на интервале (α, β), включающем в себя точку x₀, и удовлетворяющее условию (2), то функции φ(x) и ф(x) совпадают там, где они обе определены.

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать - это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам - изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

• Общий интеграл, семейство кривых
• Дифференциальные уравнения первого порядка
• Решение задачи Коши для ДУ
• Дифференциальные уравнения второго порядка
• Задачи на составление дифференциальных уравнений
• Нелинейные дифференциальные уравнения

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

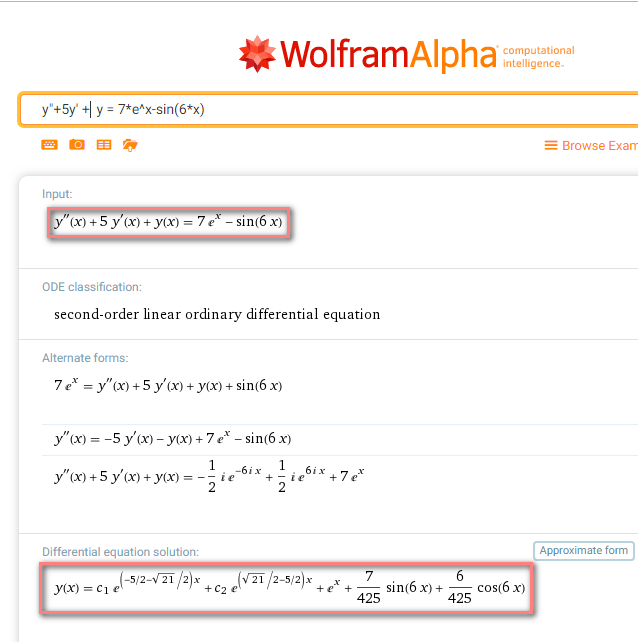
Если вы забьете в поисковик что-то вроде "решить дифференциальное уравнение онлайн", то получите десятки ссылок на сайты, обещающие именно это.

Выводы? Бесплатно и полно и онлайн - не бывает. Хотите получать полные решения - используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы - там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy'+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y'=-y/x \quad (x \ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y'-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y'=y-1.$

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y'' +1 =(y')^2, \, y(1/3)=1, \, y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y'= \frac<2y-x><2x+y>, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y'''=x+\cos x, \quad y(0)=0, y'(0)=0, y''(0)=0. $$

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y''+4y'+4y=xe^<2x>.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y''-3y'=\frac<9e^<-3x>><3+e^<-3x>>, \quad y(0)=4\ln 4, y'(0)=3(3\ln 4-1). $$

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy'+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy'+8y^2=0.$

Обычно задача Коши интересует студентов, которым задали найти решение дифференциального уравнения, когда заданы начальные условия. Иногда задачу формулируют по другому - требуется найти частное решение дифференциального уравнения. Стандартный способ решения такой задачи: сразу находят общее решение (с константами), потом в него подставляют начальные условия и определяют значения констант. И на последнем шаге значения констант подставляют в общее решение - получается частное решение, удовлетворяющее заданным начальным значениям.

Используя наш калькулятор можно сразу получить решение задачи Коши. Для этого вводится само дифуравнение и через запятую начальные условия. Пример команды смотрите ниже. Решение записано в блоке "Differential equation solution:". Для вставки команды в решатель нажмите значок вставки справа от команды, а затем нажмите кнопку "Решить".

• Решение системы трех линейных уравнений
• Калькулятор для матриц (2х2)
• Строим график в полярных координатах
• Решить систему линейных уравнений

• Проблемы изучения математики в 3 кла.
• Проверить будет ли число простым - P.
• Сумма цифр числа в Python
• Пузырьковая сортировка в Python
• Алгоритм Эвклида для НОД в Python
• Все материалы библиотеки

• Задачник по физике - Перышкин
• Скачать плагин "Редактор LaTeX" для .
• Базы данных Access
• Язык программирования Ассемблер
• Базовая система ввода - вывода BIOS
• Все файлы для скачивания

• Онлайн-решебник задач
• MathPad -математический блокнот
• LaTeX+MarkDown редактор формул
• Универсальный калькулятор
• Числовой калькулятор
• Сфоткай и добавь свою задачу
• Решения задач из Сканави
• Характеристика студента онлайн
• Диаграммы и графики онлайн
• Конструктор программ на Паскале
• Самые популярные материалы
• Доска почета: лучшие пользователи

"Салат Фибоначчи. Составлен из вчерашнего и позазавчерашеного салата. "