Небольшая семейная фирма производит два широко популярных безалкогольных напитка

Задача 1. Решить графическим методом типовую задачу оптимизации

Фирма производит два широко популярных безалкогольных напитка - "Лимонад" и "Тоник". Фирма может продать всю продукцию, которая будет произведена. Однако объем производства ограничен количеством основного ингредиента и производственной мощностью имеющегося оборудования. Для производства 1 л "Лимонада" требуется 0,02 час работы оборудования, а для производства 1 л "Тоника" - 0,04 ч. Расход специального ингредиента составляет 0,01 кг и 0,04 кг на 1 л "Лимонада" и "Тоника" соответственно. Ежедневно в распоряжении Фирмы имеется 24 ч времени работы оборудования и 16 кг специального ингредиента. Прибыль фирмы составляет 0,1 ден. ед. за 1 л "Лимонада" и 0,3 ден. ед. за 1 л "Тоника". Сколько продукции каждого вида следует производит ежедневно, если цель фирмы состоит в максимизации ежедневной работы?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум и почему?

Составим ЭММ задачи:

В рамках заданных ограничений фирма должна принять решение о том, какое количество каждого вида напитков следует выпускать. Пусть x1 - число литров Лимонада, производимое за день. Пусть x2 - число литров Тоника, производимое за день.

Определение цели и ограничений. Цель состоит в максимизации ежедневного дохода. Пусть F(x) = 0,1x1 + 0,3x2 (max) - ежедневный доход, ден. ед. Он максимизируется в рамках ограничений на количество часов работы оборудования и наличие специального ингредиента. Это целевая функция задачи - количественное соотношение, которое подлежит оптимизации.

Существуют следующие ограничения на производственный процесс:

Время работы оборудования. Для производства х1 литров Лимонада и х2 литров Тоника требуется: (0,02 х1 + 0,04 х2) часов работы оборудования ежедневно. Максимальное время работы оборудования в день составляет 24 ч, следовательно, объем производства должен быть таким, чтобы число затраченных часов работы оборудования было меньше либо равно 24 ч ежедневно. Таким образом,

,02 х1 + 0,04 х2£ 24 ч/день.

Специальный ингредиент. Производство х1 литров Лимонада и х2 литров Тоника требует (0,01 х1 + 0,04 х2) кг ингредиента ежедневно. Максимальный расход ингредиента составляет 16 кг в день, следовательно, объем производства должен быть таким, чтобы требуемое количество специального ингредиента составляло не более 16 кг в день. Таким образом,

,01 х1 + 0,04 х2 £ 16 кг/день.

Окончательная формулировка задачи линейного программирования имеет следующий вид:

(x) = 0,1x1 + 0,3x2 (max)

,02 х1 + 0,04 х2 ≤ 24

,01 х1 + 0,04 х2 ≤ 16

Ограничения задачи можно изобразить графически.

Время работы оборудования:

,02 х1 + 0,04 х2 ≤ 24 ч/день.

,02 х1 + 0,04 х2 = 24

Простейшим способом нанесения прямой на график является нахождение точек пересечения данной прямой с осями координат х1 и х2. Подставив х1 = 0 в уравнение и рассчитав значение х1, получим, что при х1 = 0, х2 = 600. Подставив х2= 0 в уравнение и рассчитав значение х1, получим, что при х2 = 0 х1 = 1200. Нанесем эти две точки на график и соединим их прямой. Для определения области, которую следует заштриховать, подставим х1= 0 и х2 = 0 в неравенство: 0,02 х1 + 0,04 х2 ≤ 24

Специальный ингредиент: 0,01 х1 + 0,04 х2 ≤ 16

Проведем прямую: 0,01 х1 + 0,04 х2 = 16

Таким же образом, подставив х1 = 0 в уравнение и рассчитав значение х1, получим, что при х1 = 0, х2 = 400. Подставив х2= 0 в уравнение и рассчитав значение х1, получим, что при х2 = 0 х1 = 1600. Нанесем эти две точки на график и соединим их прямой. Для определения области, которую следует заштриховать, подставим х1= 0 и х2 = 0 в неравенство: 0,01 х1 + 0,04 х2 ≤ 16

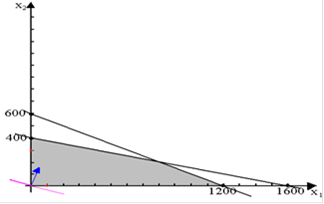
Область, отмеченная серым цветом - это допустимое множество,

которое содержит все возможные сочетания объемов производства, удовлетворяющие данным ограничениям. Координаты любой точки, принадлежащей допустимому множеству, являются возможным сочетанием объемов производства двух видов напитков, выпускаемых фирмой.

Основная процедура является общей для формулирования всех задач линейного программирования:

Шаг 1. Определение переменных задачи, значения которых нужно получить в пределах существующих ограничений.

Шаг 2. Определение цели и ограничений на ресурсы.

Шаг 3? Описание цели через переменные задачи.

Шаг 4. Описание ограничений через переменные задачи.

Хотя на применение данной процедуры не влияет число переменных в задаче линейного программирования, рассмотрим сначала задачу с двумя переменными.

Шаг 2. Определение цели и ограничений. Цель состоит в максимизации ежедневного дохода. Пусть Р — ежедневный доход, ф. ст. Он максимизируется в рамках ограничений на количество часов работы оборудования и наличие специального ингредиента.

Шаг 3. Выразим цель через переменные:

Это целевая функция задачи — количественное соотношение, которое подлежит оптимизации.

Шаг 4. Выразим ограничения через переменные. Существуют следующие ограничения на производственный процесс:

Других ограничений нет, однако разумно предположить, что фирма не может производить напитки в отрицательных количествах, поэтому:

в) Условие неотрицательности:

Окончательная формулировка задачи линейного программирования имеет следующий вид. Максимизировать:

Сначала необходимо сформулировать задачу линейного программирования.

Шаг 1. Идентификация переменных. Необходимо произвести х деталей типа X и у деталей типа Y в неделю.

Шаг 2. Какова цель задачи? Каковы ограничения на процесс производства? Цель состоит в максимизации общего дохода за неделю. Производственный процесс ограничивается уровнем:

б) производственной мощности — для каждого типа деталей существует отдельное ограничение по производственной мощности. Оборудование позволяет выпускать не более 2250 деталей типа X и 1750 типа Y в неделю.

в) металлических стержней — максимальный их уровень составляет 10000 кг в неделю.

г) листового металла — максимальный уровень этого ресурса равен 10000 кг в неделю.

Кроме того, существуют ограничения на минимальный объем производства деталей каждого вида:

а) постоянные заказы — число произведенных деталей X должно быть достаточным для удовлетворения размера постоянных заказов.

Шаг 3. Целевая функция. Пусть Р — общий доход за неделю, ф. ст., где

Шаг 4. Ограничения на производственный процесс. Для каждого ограничения на ресурсы, необходимые для производства х деталей типа X и у деталей типа Y в неделю, ниже приведены количества и соответствующие им максимальные уровни наличных ресурсов.

Требуемое количество металлических

Окончательная формулировка задачи линейного программирования имеет вид: Производится х деталей типа X и у деталей типа У в неделю. Максимизировать:

Теперь рассмотрим задачу, число переменных в которой больше двух. Общая схема формулировки и в этом случае остается неизменной.

О Пример 12.3. Завод по производству электронного оборудования выпускает персональные компьютеры и системы подготовки текстов. В настоящее время освоены четыре модели:

а) "Юпитер" — объем памяти 512 Кбайт, одинарный дисковод;

б) "Венера" — объем памяти 512 Кбайт, двойной дисковод;

в) "Марс" — объем памяти 640 Кбайт, двойной дисковод;

г) "Сатурн" — объем памяти 640 Кбайт, жесткий диск.

Построить задачу линейного программирования для изложенной проблемы производства изделий в ассортименте, если цель состоит в максимизации общего ежемесячного дохода.

Таблица 12.1. Время, требуемое на обработку каждой модели каждом цехе

Шаг 2. Какова цель задачи? Каковы ограничения на производственный процесс? Цель состоит в максимизации общего дохода за месяц. Объем производства ограничен размером фонда рабочего времени по каждому цеху и возможностью продажи компьютеров каждой модели. -

Шаг 3. Целевая функция задачи. Пусть Р (ф. ст.) — общий доход в месяц, тогда:

в условиях ограничений, указанных выше.

Максимизация целевой функции осуществляется в условиях ограничений на

Чтобы решить задачу линейного программирования, ограничения обычно преобразовывают таким образом, чтобы переменные находились только в левой части любого неравенства. Результаты этого преобразования представлены ниже. Окончательная форма задачи линейного программирования имеет следующий вид:

Максимизируется общая сумма годового процентного дохода, т.е.:

Во всех четырех приведенных выше примерах целевую функцию требовалось максимизировать. На стадии постановки задачи процедура не меняется, если целью является минимизация некоторого показателя. Примеры таких задач приводятся в конце данной главы.

Фирма производит два безалкогольных широко популярных напитка " Колокольчик" и "Буратино". Для производства 1 л. " Колокольчика требуется 0, 002 ч работы оборудования, а для " Буратино" - 0,04 ч, а расход специального ингредиента на них составляет 0,01 кг и 0, 04 кг на 1 л соответственно. Ежедневно в распоряжении фирмы 16 кг специального ингредиента и 24 ч работы оборудования. Доход от продажи 1 л

" Колокольчика" составляет 0,25 руб., а " Буратино" - 0,35 руб.

Определите ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от их продажи.

1) Составим математическую модель данной задачи:

Пусть X₁ - количество " Колокольчиков";

Х₂ - количество " Буратино", тогда как необходимо определить ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от их продажи, то целевая функция:

2) Графическое решение задачи:

Представим каждое неравенство в виде равенства, т.е имеем уравнения прямых. Построим их, тогда система ограничений запишется в виде:

Преобразуем систему неравенств ( выразим Х₂ через Х₁)

Построим на плоскости ( х₁,х₂) область допустимых значений согласно системе неравенств

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Всероссийский заочный финансово-экономический институт

Список использованной литературы…………………………………..30

Решить графическим методом типовую задачу оптимизации.

max f ( ) = 0,10x 1 + 0,30x 2

при условии выполнения ограничений:

Решаем задачу графическим методом:

Областью допустимых решений системы является многоугольник ОАВС.

Построим линию уровня 0,10 x 1 + 0,30 x 2 и вектор .

При перемещении линии уровня в направлении вектора значении функции возрастает. Наибольшее значение достигается в точке B.

x 1 + 4·200 = 1600

Проверим правильность расчетов с помощью средств MS Excel:

1. Ввели зависимость для целевой функции и ограничений:

3. Из меню Сервис выберали Поиск решения.

Назначили целевую функцию, ввели ограничения и на вкладке Параметры установили Линейная модель и Неотрицательные значения.

4. Щелкнули Выполнить.

При решении задачи на min линию уровня следует сдвигать в противоположную сторону от вектора . Наименьшее значение будет достигнуто в точке О (0;0). Значит x 1 = 0, x 2 = 0, . Это значит, что не надо ничего выпускать и прибыль будет равна 0.

Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования.

Для изготовления трех видов продукции используют четыре вида ресурсов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Нормы расхода ресурсов на единицу продукции

Основная процедура является общей для формулирования всех задач линейного программирования:

Шаг 1. Определение переменных задачи, значения которых нужно получить в пределах существующих ограничений. Шаг 2. Определение цели и ограничений на ресурсы. Шаг 3- Описание цели через переменные задачи. Шаг 4. Описание ограничений через переменные задачи.

□ Пример 12.1.Небольшая семейная фирма производит два широко популярных безалкогольных напитка — "Pink Fizz" и "Mint Pop". Фирма может продать всю продукцию, которая будет произведена, однако объем производства ограничен количеством основного ингредиента и производственной мощностью имеющегося оборудования. Для производства 1 л "Pink Fizz" требуется 0,02 ч работы оборудования, а для производства 1 л "Mint Pop" — 0,04 ч. Расход специального ингредиента составляет 0,01 кг и 0,04 кг на 1 л "Pink Fizz" и "Mint Pop" соответственно. Ежедневно в распоряжении фирмы имеется 24 ч времени работы оборудования и 16 кг специального ингредиента. Доход фирмы составляет 0,10 ф. ст. за 1 л "Pink Fizz" и 0,30 ф. ст. за 1 л "Mint Pop". Сколько продукции каждого вида следует производить ежедневно, если цель фирмы состоит в максимизации ежедневного дохода?

Решение Шаг 1. Определение переменных. В рамках заданных ограничений фирма должна принять решение о том, какое количество каждого вида напитков следует выпускать. Пусть р — число литров "Pink Fizz", производимое за день. Пусть m — число литров "Mint Pop", производимое за день.

402 Ч. 4. Моделирование в бизнесе

Шаг 2. Определение цели и ограничений. Цель состоит в максимизации ежедневного дохода. Пусть Р — ежедневный доход, ф. ст. Он максимизируется в рамках ограничений на количество часов работы оборудования и наличие специального ингредиента. Шаг 3- Выразим цель через переменные:

Р = 0,10 р + 0,30 m (ф. ст. в день).

Это целевая функция задачи — количественное соотношение, которое подлежит оптимизации.

Шаг 4. Выразим ограничения через переменные. Существуют следующие ограничения на производственный процесс:

а) Время работы оборудования. Для производства р литров "Pink Fizz" и га
литров "Mint Pop" требуется: (0,02 р + 0,04 т) часов работы оборудова
ния ежедневно. Максимальное время работы оборудования в день состав
ляет 24 ч, следовательно, объем производства должен быть таким, чтобы
число затраченных часов работы оборудования было меньше либо равно
24 ч ежедневно. Таким образом,

0,02 р + 0,04 m £ 24 ч/день.

б) Специальный ингредиент. Производство р литров "Pink Fizz" и m литров
"Mint Pop" требует (0,01 р + 0,04 го.) кг ингредиента ежедневно. Макси
мальный расход ингредиента составляет 16 кг в день, следовательно,
объем производства должен быть таким, чтобы требуемое количество
специального ингредиента составляло не более 16 кг в день. Таким
образом,

0,01 р + 0,04 m Z 16 кг/день.

в) Условие неотрицательности:

р Z 0, m Z 0.

Окончательная формулировка задачи линейного программирования имеет следующий вид. Максимизировать:

Р = 0,10 р + 0,30 m (ф. ст. в день)

Окончательная формулировка задачи линейного программирования такова: каждый месяц производится j, v, га и s единиц компьютеров типа "Юпитер", "Венера", "Марс" и "Сатурн" соответственно. Максимизировать:

Р = 15 j + 30 v + 120 m + 130 s (ф. ст. в месяц)

в условиях ограничений, указанных выше.

О Пример 12.4.Менеджер по ценным бумагам намерен разместить 100000 ф. ст. капитала таким образом, чтобы получать максимальные годовые проценты с дохода. Его выбор ограничен четырьмя возможными объектами инвестиций: А, В, С и D. Объект А позволяет получать 6% годовых, объект В — 8% годовых, объект

лдб Ч. 4. Моделирование в бизнесе

q — 10%, а объект D — 9% годовых. Для всех четырех объектов степень риска и условия размещения капитала различны. Чтобы не подвергать риску имеющийся капитал, менеджер принял решение, что не менее половины инвестиций необходимо вложить в объекты А и В. Чтобы обеспечить ликвидность, не менее 25% общей суммы капитала нужно поместить в объект D. Учитывая возможные изменения в политике правительства, предусматривается, что в объект С следует вкладывать не более 20% инвестиций, тогда как особенности налоговой политики требуют, чтобы в объект А было вложено не менее 30% капитала. Сформулируем для изложенной проблемы распределения инвестиций модель линейного программирования.

Решение Вкладывается а ф. ст. в объект А, Ь ф. ст. — в объект В, с ф. ст. — в объект С и d ф. ст. — -в объект D. Целью является максимизация общей суммы годовых процентов с дохода. На распределение инвестиций наложены ограничения, связанные с отсутствием риска, ликвидностью, политикой правительства и системой налогообложения. Обозначим через R общую сумму годового процентного дохода, тогда:

R = 0,06 а + 0,08 Ь + 0,10 с + 0,09 d (ф. ст. в год).

Максимизация целевой функции осуществляется в условиях ограничений на

Общую сумму инвестиций: a + b + c + di 100000 ф. ст.

Отсутствие риска: а+Ьг 0,05 (а + b + с + d)

Ликвидность: d i. 0,25 (а + b + с + d)

Правительственную политику: с S 0,2 (а + b + с + d)

Систему налогообложения: а £ 0,3 (а + b + с + d)

Неотрицательность: а, Ь, с, d £ 0.

Чтобы решить задачу линейного программирования, ограничения обычно преобразовывают таким образом, чтобы переменные находились только в левой части любого неравенства. Результаты этого преобразования представлены ниже. Окончательная форма задачи линейного программирования имеет следующий вид:

Вкладывается а ф. ст. в объект А,

b ф. ст. в объект В,

с ф. ст. в объект С,

d ф. ст. в объект D. Максимизируется общая сумма годового процентного дохода, т.е.:

R=0,06 а + 0 ,08 b + 0,10 с + 0,09 d (ф. ст. в год)

в условиях следующих ограничений (ф. ст.):

Общая сумма инвестиций: а + b+ c+ d £ 100000

Отсутствие риска: 0,5 а + 0,5 b - 0,5 с - 0,5 d £ 0

Ликвидность: -0,25 а -0,25Ь -0,25 с + 0,75d £ 0

политика: -0,2 а - 0,2 Ь + 0,8 с - 0,2 d SO

Система налогообложения: 0,7 а - 0,3 b - 0,3 с - 0,3 d > 0

Условие неотрицательности: а, Ь, с, d £ 0

Гл. 12. Линейное программирование 407

Задача 2. Завод-производитель высокоточных элементов для автомобилей выпускает два различных типа деталей: Х и Y. Завод располагает фондом рабочего времени в 4000 чел.-ч. в неделю. Для производства одной детали типа X требуется 1 чел.-ч, а для производства одной детали типа Y — 2 чел.-ч. Производственные мощности завода позволяют выпускать максимум 2250 деталей типа Х и 1750 деталей типа Y в неделю. Каждая деталь типа Х требует 2 кг металлических стержней и 5 кг листового металла, а для производства одной детали типа Y необходимо 5 кг металлических стержней и 2 кг листового металла. Уровень запасов каждого вида металла составляет 10000 кг в неделю. Кроме того, еженедельно завод поставляет 600 деталей типа Х своему постоянному заказчику. Существует также профсоюзное соглашение, в соответствии с которым общее число производимых в течение одной недели деталей должно составлять не менее 1500 штук.

Сколько деталей каждого типа следует производить, чтобы максимизировать общий доход за неделю, если доход от производства одной детали типа Х составляет 30 ф. ст., а от производства одной детали типа Y — 40 ф. ст.?

Задача 3. Компания производит полки для ванных комнат двух размеров - А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В - 30 мин; машину можно использовать 160 час в неделю. Если прибыль от продажи полок типа А составляет 3 денежных единицы, а от полок типа В - 4 ден. ед., то сколько полок каждого типа следует выпускать в неделю?

Задача 4. Предприятие производит 3 вида продукции: А1, А2, А3, используя сырьё двух типов. Известны затраты сырья каждого типа на единицу продукции, запасы сырья на планируемый период, а также прибыль от единицы продукции каждого вида.

Сырьё	Затраты сырья на единицу продукции	Запас сырья
А1	А2	А3
I	3,5	4,2
II
Прибыль от ед. прод.

Сколько изделий каждого вида необходимо произвести, чтобы получить максимум прибыли?
Определить статус каждого вида сырья и его удельную ценность.
Определить максимальный интервал изменения запасов каждого вида сырья, в пределах которого структура оптимального плана, т.е. номенклатура выпуска, не изменится.
Определить количество выпускаемой продукции и прибыль от выпуска при увеличении запаса одного из дефицитных видов сырья до максимально возможной (в пределах данной номенклатуры выпуска) величины.
Определить интервалы изменения прибыли от единицы продукции каждого вида, при которых полученный оптимальный план не изменится.

Задача 5. Колхоз имеет возможность приобрести не более 19 трехтонных автомашин и не более 17 пятитонных. Отпускная цена трехтонного грузовика - 4000 руб., пятитонного - 5000 руб. Колхоз может выделить для приобретения автомашин 141 тысяч рублей. Сколько нужно приобрести автомашин, чтобы их суммарная грузоподъемность была максимальной?
Задачу решить графическими и аналитическими методами.

Задача 6. Менеджер по ценным бумагам намерен разместить 100000 ф. ст.

капитала таким образом, чтобы получать максимальные годовые проценты с дохода. Его выбор ограничен четырьмя возможными объектами инвестиций: А, В, С и D. Объект А позволяет получать 6% годовых, объект В — 8% годовых, объект С — 10%, а объект D — 9% годовых. Для всех четырех объектов степень риска и условия размещения капитала различны. Чтобы не подвергать риску имеющийся капитал, менеджер принял решение, что не менее половины инвестиций необходимо вложить в объекты А и В. Чтобы обеспечить ликвидность, не менее 25% общей суммы капитала нужно поместить в объект D. Учитывая возможные изменения в политике правительства, предусматривается, что в объект С следует вкладывать не более 20% инвестиций, тогда как особенности налоговой политики требуют, чтобы в объект А было вложено не менее 30% капитала. Сформулируйте для изложенной проблемы распределения инвестиций модель линейного программирования.

Контрольная Решить графическим методом типовую задачу оптимизации Тип работы: Контрольная. Добавлен: 24.12.2013. Год: 2013. Страниц: 24. Уникальность по antiplagiat.ru:

Рис.1 Решение задачи

Построим прямые, соответствующие ограничениям задачи: первая прямая имеет вид 0,02х1 + 0,04 х2 = 24, решением ее служат точки (1200;0)
и (0;400); вторая прямая имеет вид 0,01х1 + 0,04 х2 = 16, решением ее служат точки (1600;0) и (0;600).
Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений.

Рис.2Область допустимых решений

На рисунке 1 заштрихована область допустимых значений.Для определения движения к оптимуму построим вектор-градиент. При максимизации функции движемся вдоль вектора-градиента.

Решим систему уравнений:
0,02х1 + 0,04 х2 = 24;
0,01х1 + 0,04 х2 = 16.
х1 + 4х2 = 1600
х1=1600 - 4х2
0,02 (1600 - 4х2) + 0,04х2 = 24
32 ? 0,08х2+0,04х2 = 24
?0,04х2 = ?8
Х2 = 8?0,04=200 ? х1=1600?4?200=800
ЦФ(800; 200)= 0,1 ? 800 + 0,3 ? 200= 140 (ден. ед.)

Задача 2.
Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования.
Для изготовления трех видов продукции используют четыре вида ресурсов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Вид ресурсов Нормы расхода ресурсов на ед. продукции Запасы ресурсов
I вид II вид III вид
Труд Сырье 1 Сырье 2 Оборудование 3 20 10 0 6 15 15 3 4 20 20 5 2000 15000 7400 1500
Цена изделия 6 10 9

Требуется:
1) Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
2) Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
3) Пояснить нулевые значения переменных в оптимальном плане.
4) На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка и план выпуска продукции при увеличении запаса ресурса первого вида на 24ед.;
- оценить целесообразность включения в план изделия четвертого вида ценой 11ед., если нормы затрат ресурсов 8, 4, 20 и 6 ед.

Решение:
1) Сформулировать прямую .

Гармаш А.Н., Гусарова О.М., Орлова И.В., Якушев А.А.Экономико-математические методы и прикладные модели: Компьютерный практикум и руководство к выполнению лабораторной работы по теме "Оптимизационные экономико-математические модели. Методы получения оптимальных решений" -М.: ВЗФЭИ, 2005.
Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде Excel. Практикум. - М.: Финстатинформ, 2009.
Орлова И.В. Экономико-математическое моделирование. Практическое пособие по решению задач - М.: ВЗФЭИ. Вузовский учебник, 2004.
Федосеев В.В., Гармаш А.Н., Орлова И.В., Половников В.А. Экономико-математические методы и прикладные модели. 2-е изд. - М.: ЮНИТИ-ДАНА, 2006.
Половников В.А., Орлова И.В., Гармаш А.Н. Экономико-математические методы и прикладные модели: Методические указания по выполнению контрольной работы, темы и задачи. - М.: ВЗФЭИ, 2008.

* Примечание. Уникальность работы указана на дату публикации, текущее значение может отличаться от указанного.

Тема: Контрольная по Методам оптимальных решений Вариант 10

Вуз: Финансовый университет

Год и город: Москва 2013

ЗАДАЧА 1

Решить графическим методом типовую задачу оптимизации.

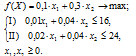
Задачу решаем графическим методом.

Строим область допустимых решений задачи (см. рисунок). Данные для ее построения приведены в таблице:

Точки для построения граничной прямой

Выполнение неравенства в контрольной точке (0; 0)

Стоим вектор-градиент целевой функции задачи. За его начало принимаем точку (0; 0), тогда концом вектора-градиента будет являться точка с координатами, равными коэффициентам целевой функции по соответствующим координатным осям — (0,1; 0,3). Перпендикулярно вектору-градиенту через точку его начала строится линия нулевого уровня целевой функции — прямая, в каждой точке которой целевая функция принимает нулевое значение: f(X)=0.

Для определения положения точки максимума целевой функции линия, параллельная линии нулевого уровня, смещается в направлении вектора-градиента, до тех пор, пока она не покинет область допустимых решений. Предельная точка области допустимых решений при этом движении и является точкой максимума.

В нашей задаче — это точка B, образованная пересечением граничных прямых ограничений I и II. Ее координаты определяются решением системы уравнений этих прямых:

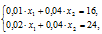
Таким образом, для получения максимально возможной в данных условиях выручки 140 руб. следует производить 800 л напитка “Лимонад” X₁ и 200 л напитка “Тоник” X₂.

Решение данной задачи линейного программирования на минимум лишено экономического смысла, так как выручку от реализации продукции стремятся получить наибольшей, а не наименьшей. Однако математически эта задача имеет решение и на минимум: наименьшее значение в области допустимых решений целевая функция принимает в точке (0; 0), и это значение равно

ЗАДАЧА 2

Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования

Нормы расхода ресурсов на ед. продукции

Требуется:

Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
Пояснить нулевые значения переменных в оптимальном плане.
На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка и план выпуска продукции при увеличении запаса ресурса первого вида на 24 единицы;
- оценить целесообразность включения в план изделия четвертого вида ценой 11 денежных единиц, если нормы затрат ресурсов 8, 4, 20 и 6 единиц.

Решение. 1. Данная задача оптимизации является задачей линейного программирования. Обозначим количество выпускаемых единиц продукции I, II, III соответственно как х₁, х₂, х₃. Целевой функцией задачи является общая стоимость выпускаемой продукции, которая должна быть наибольшей. Число ограничений задачи равно числу ресурсов, используемых для изготовления изделий — 4. Дополнительно вводится условие неотрицательности переменных. Зная цены изделий, нормы их расхода и запасы ресурсов, формулируем математическую модель исходной задачи линейного программирования:

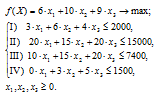
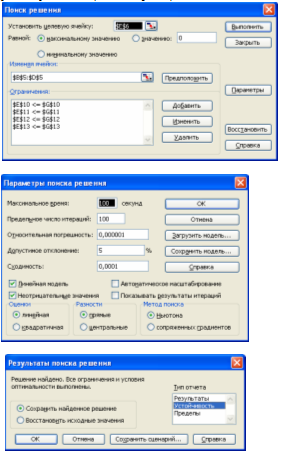
(для копирования снимка окна в буфер обмена данных используется комбинация клавиш Alt + Print Screen).

Использование надстройки позволило получить значения переменных оптимального плана выпуска изделий: Х*=(520; 0; 110). Целевая функция имеет наибольшее для данных условий задачи значение f(X*)=4110 (прил. 1).

Таким образом, для получения наибольшей выручки от реализации продукции следует производить x₁*=520 изделий I, x₃*=110 изделий III и не производить изделия II (x₂*=0).

2. Обозначим двойственные оценки ресурсов I, II, III, IV как y₁, y₂, y₃, y₄ соответственно. Целевой функцией двойственной задачи является общая стоимость запасов ресурсов в двойственных оценках, которая должна быть наименьшей. Число ограничений двойственной задачи равно числу переменных исходной задачи — 3. Математическая модель двойственной задачи имеет вид:

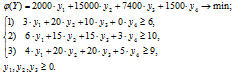
Наименьшее значение целевой функции двойственной задачи

совпадает (в пределах погрешности округления) с наибольшим значением целевой функции исходной задачи f(X*).

3. Выпуск изделий II невыгоден для данных условий задачи. Это объясняется тем, что стоимость ресурсов на изготовление единицы этой продукции в теневых ценах превышает цену реализации:

4. Проанализируем использование ресурсов в оптимальном плане. Для этого подставим в ограничения исходной задачи значения переменных оптимального плана Х*=(520; 0; 110) и проверим выполнение неравенств:

Видно, что ресурсы I и III используются в оптимальном плане полностью, т. е. являются дефицитными. На это обстоятельство указывает и то, что теневые цены этих ресурсов больше нуля (y₁*>0; y₃*>0). Самым дефицитным является ресурс I, так как он имеет наибольшую теневую цену (y₁*=1,5); наименее дефицитен ресурс III (y₃*=0,15).

Ограниченные запасы дефицитных ресурсов I и III сдерживают рост объемов выпускаемой продукции и наибольшей выручки от ее реализации. Увеличение объема ресурса I на одну единицу при неизменных объемах других ресурсов ведет к росту наибольшей выручки на 1,5 руб., увеличение объема ресурса III на единицу — на 0,15 руб.

Ресурсы II и IV являются недефицитными (y₂*=0; y₄*=0), т. е. избыточными в оптимальном плане. Увеличение объемов этих ресурсов не повлияет на оптимальный план выпуска продукции и не увеличит ее общую стоимость.

Для определения целесообразности включения в план выпуска еще и изделия IV с заданными характеристиками рассчитаем стоимость ресурсов на изготовление единицы этого изделия в теневых ценах и сравним это значение с ценой реализации:

Следовательно, продукцию IV выпускать невыгодно, так как она поглощает часть дефицитных ресурсов и тем самым сдерживает рост выпуска выгодной продукции. Это, в свою очередь, препятствует увеличению общей стоимости выпускаемых изделий. Если бы изделие IV реализовывалось по цене равной или большей 15 руб., то его производство было бы выгодным.

1) рабочий лист EXCEL;

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы

Читайте также: